Discrete Event Systems Based Robotic Task Modeling
Most of the existing robotic task models are not based on formal approaches, are concerned only with a small number of behaviors and are typically tailored to the task at hand. We have proposed, back to 1998 [1] a systems-theory-based task modeling approach for general robotic tasks which enables a systematic approach to modeling, analysis and design, scaling up to realistic applications, providing methods for logical verification, stochastic performance, and design from specifications, as well as execution improvement over time through learning. Our approach is based on using discrete event systems (DES) models, mainly Petri nets and finite state automata, for robot plans representation. This particular representation enables using all the available DES analysis and design tools to handle robotic task formal analysis and design.
Representing robot plans by DES
A plan is composed of several actions, running concurrently or sequentially. Action sequences, loops, subplans running in separate robots from a team, are possible examples of plans under the above definition.
In our robotic task model, theree entities are defined:
- propositions (predicates with instantiated arguments), e.g., see(object), in(robot1, room3)
- primitive actions (may have arguments, but must be also bound to some actual object), e.g., move2object, standby, catch(glass)
- events, e.g., start_standby, button_pressed, wheel_failure
The subset of events corresponding to starting a primitive action are controllable. Those corresponding to occurrences the robot(s) can not start or stop (e.g., due to the environment dynamics, ot to other agents’ actions) are uncontrollable.
When using finite state automata (FSA) representations, propositions and primitive actions are collected in states, and events are associated to transitions.
Petri net (PN) models of robotic tasks distribute the state across the PN places. Some places represent propositions, other represent primitive actions. When one such place has a token, the model signals that a proposition is true or an associated primitive action is running, respectively. Events are associated to transitions.
One may have different FSA or PN views, namely a logical untimed view, where the model can be studied based on the language (event strings) it generates, or a stochatic timed view, where time is of concern, and considered stochastically distributed. If stochastic interevent time is associated to transitions, one gets stochatic timed FSA or PN. If the event time pdf is exponential, both the FSA and the PN reachability graph can be made equivalent to Markov Chanis. If we consider the controllable event subset as subject to decisions by a higher command level, the model ends up being a Markov Decision Process (MDP), and dynamic programming or reinforcement learning solutions can be applied to determine the optimal plan in terms of minimizing some cost function, where costs are associated to primitive actions, and may include thprimitive action reliability.
Institutional Controllers for Distributed Robotic Systems
A formalism to represent institutions by Petri nets, within the Institutional Robotics framework, has been developed. We have assessed the ability of our formalism to replicate results obtained with other approaches in simulation and with swarms of up to 40 real e-puck robots. In particular, we have worked on a case study concerned with a swarm of simple robots which has to maintain wireless connectivity and compare results from realistic simulations performed with the institutional controller to those performed with a Finite State Automata controller. Petri net based institutional controllers can be used in modeling and analyzing the distributed robotic system they control by providing the necessary structure to build macroscopic models of that system, and studying their stochastic performance properties.
Robotic task supervision using LTL
Supervisory Control of DES consists of restricting the behavior of a DES in order to achieve a set of specifications, usually expressed as required and/or admissible languages, with respect to the original language of the unsupervised system.
In this work, we use Linear-Time Temporal Logic (LTL), an extension of Propositional Logic which allows reasoning over an infinite sequence of states, to specify the performance objectives for a given DES in a more natural language, and build a supervisor that restricts the DES’ behavior to those objectives by construction.
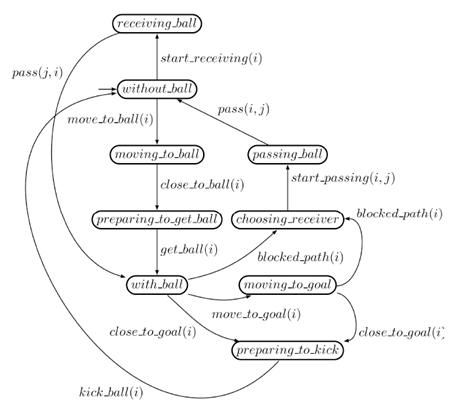
The figure depicts an FSA representing the different possible behaviors for a single soccer robot. For instance, when the robot has the ball (state with_ball) it may decide to prepare to get close to the ball to prepare to kick it, to move with the ball towards the goal, or to prepare a pass, choosing the receiver, in case the uncontrollable event blocked_path occurs. This FSA can be composed with similar FSA representing the behaviors of homogeneous teammates. An LTL specification prevents any robot in the team from receiving a pass until one of them is selected as the receiver by the passer. Another situation is when the robot does not have the ball: the options are either moving towards the ball to catch it or getting ready to receive a pass. Again, an LTL formula can be used to avoid that more than one robot move towards the ball simultaneously. More details in [5].
Robotic task performance analysis using Petri nets
For both models, it is convenient to build up a separate environment model of the same type, i.e., an FSA or a PN model of the environment, where transitions are associated to robot controllable events (thus representing its effects), or uncontrollable events (thus representing environment natural events, including those caused by other agents starting their own actions.
In fact, especially for PNs, the key issue is that one can build a large complex robotic task model by connecting simple PN modules which represent the dynamic of the robot subsystems (e.g., the PN representing the navigation system, or the perception system status). Macro-actions can also encapsulate action compositions. And the whole robot plan, represented by a PN, can be composed with the environment pan, also represented by a PN (in fact, this composition between the robot plan and the environment models is also true for FSA representations).
Robotic task performance analysis should be performed over the above closed loop model of the robot situated in its environment. Two main classes of analysis problems are:
- qualitative/logical analysis: such as determining PN liveness (is the plan resetable, can the robot recover from an error?), boundedness (are we using too many resources, e.g., calling a primitive action to run concurrently in a number of processors – or robots – larger than those available?), blocking (deadlocks, livelocks)
- quantitative/stochastic performance analysis: is a plan robust to changes of primitive action reliability around their nominal values? what is the probability of succes of a plan, given the reliability of its composing primitive actions?
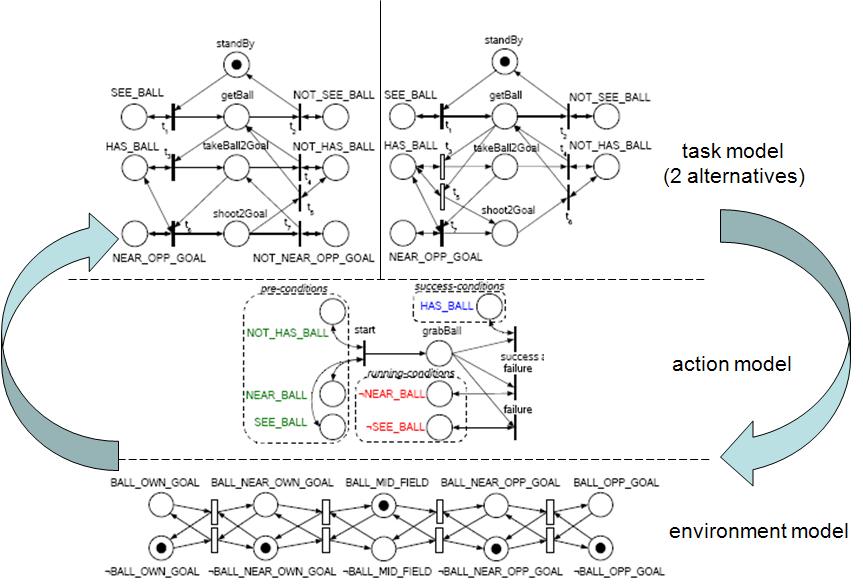
Cooperative plan representation and execution
Petri net plan representations are especially adequate to represent plans for cooperative robots. In this case, places must also represent communicated messages (sent and received), which in fact represent again predicates which, when their arguments are instantiated, become true or false propositions. Examples: waiting4you_sent, waiting4you_received, arriving_sent, arriving_received. Two types of communicated signals are relevant for cooperation (coordination + teamwork): those required for synchronization, and those required for commitment.
Synchronization concerns coordination, e.g., two robots transporting a bar and exchanging signals to avoid that one of them advances too much ahead or lags behind. One example in soccer robots can be seen in this video animation of a pass.
We have been using Petri nets to program individual and relational behaviors in the SocRob project with soccer robots, with synchronization and commitment. Commitment is based on the formalism of Cohen’s and Levesque’s joint commitment theory, and essentially assures teamwork, i.e., once two or more robots get involved in a relational behavior, they mutually commit to inform their involved teammates if the joint goal became irrelevant or can not be reached anymore (e.g., due to a failure of one of them to proceed with its part of the behavior).
The following two videos show 2 robots of our RoboCup ISocRob MSL team performing a pass, both in simulation and reality (the same code is used in both cases).
A similar concept was applied to the ISocRob 4LL team, with 2 AIBOs exchanging ball passes – see video, including simultaneous PN execution. This was joint work with Daniele Nardi’s group, at U. Rome “La Sapienza” [6][7].
Stochastic hybrid automata model of large robot populations
We have introduced a novel approach to the study of the dynamics of molecule expression level in large-size cell populations, whose goal is to understand how individual cell behavior propagates to population dynamics. In fact, the results obtained can be used to study the dynamics of (cell) populations in general, and we have also extended it to model robot swarms, and to come up with optimal stochastic control laws for them.
A Hybrid Automaton framework is used, where each discrete state corresponds to a macro state of the (cell, robot) population, and the continuous state to the micro state of each element in the population. The transitions between discrete/macro states are stochastic, and their rates are the most relevant parameters of the model.
For the cell populations, this approach enables the simultaneous modeling of the formation and dissociation of cell-to-cell conjugations, and the molecular processes they control. Serial encounters among the cells are described by a stochastic approach under which the cell distribution over the state space is modeled and the dynamics of the state probability density functions is modeled by a partial differential equation. This work was motivated by the investigation of T-cell receptor expression distribution. These receptors are essential for the antigen recognition and the regulation of the immune system. [9]
For robot/agent populations, this resulted in an approach to the modeling and control of swarms, i.e., multi-robot/agent populations composed of a large number of robots/agents. Beyond the population dynamics modeling, the control problem of maximizing the probability of robotic presence in a given region was introduced. The Minimum Principle for the optimal control of partial differential equations was exploited to solve this problem and it was applied to the mission control of a simulated large robotic population. [8]
This work was mainly the result of Dejan Milutinovic’s PhD thesis, published in a Springer STAR Series book [10].
Prof. Michael Athans (Emeritus Professor at MIT) was also involved in the co-supervision of Dejan, and this work started up a collaboration with Instituto Gulbenkian de Ciência, namely with Prof. Jorge Carneiro, coordinator of the Theoretical Immunology group.
References
[1] P. Lima, H. Grácio, V. Veiga, A. Karlsson, “Petri Nets for Modeling and Coordination of Robotic Tasks”, Proc. of IEEE International Conference on Systems, Man, and Cybernetics, San Diego, USA, 1998
[2] D. Milutinovic, P. Lima, “Petri Net Models of Robotic Tasks”, Proc. ICRA2002 – IEEE International Conference on Robotics and Automation, Washington D.C., USA, 2002
[3] H. Costelha, P. Lima, “Modeling, Analysis and Execution of Robotic Tasks using Petri Nets”, Proc. of IROS 2007 – IEEE International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 2007
[4] H. Costelha, P. Lima, “Modeling, Analysis and Execution of Multi-Robotic Tasks using Petri Nets”, Proc. of AAMAS 2008 – Proceedings of the 7th international joint conference on Autonomous agents and multiagent systems, Lisbon, Portugal, 2008
[5] B. Lacerda, P. Lima, “Linear-Time Temporal Logic Control of Discrete Event Models of Cooperative Robots”, Journal of Physical Agents, Vol. 2, No. 1, Special Issue on Multi-Robot Systems, 2008
[6] P. F. Palamara, V. A. Ziparo, L. Iocchi, D. Nardi, Pedro Lima, “Teamwork Design Based on Petri Net Plans”, Proc. of RoboCup International Symposium 2008, Suzhou, China, 2008
[7] V. Ziparo, L. Iocchi, P. Palamara, Hugo Costelha, D. Nardi, “PNP: A Formal Model for Representation and Execution of Multi-Robot Plans”, Proc. of AAMAS 2008 – 7th International Joint Conference on Autonomous Agents and Multi-Agent Systems, Estoril, Portugal, 2008
[8] D. Milutinovic, Pedro Lima, “Modeling and Optimal Centralized Control of a Large-Size Robotic Population”, IEEE Transactions on Robotics, Vol. 22, Issue: 6, pp.1280-1285, 2006
[9] D. Milutinovic, J. Carneiro, M. Athans, P. Lima, “Modeling Dynamics of Cell Population Molecule Expression Distribution”, Journal of Non-Linear Analysis: Hybrid Systems and Applications, Elsevier, Vol. 1, Issue 1, pp. 81-94, 2007
[10] D. Milutinovic, P. Lima, “Cells and Robots – Modeling and Control of Large-Size Agent Populations”, Springer Tracts in Advanced Robotics (STAR) Series , Vol. 32, 2007
[11] Hugo Costelha, Pedro Lima, “Robot task plan representation by Petri nets: modelling, identification, analysis and execution”, Autonomous Robots, 2012, DOI 10.1007/s10514-012-9288-x, 2012
[12] Bruno Lacerda, Pedro Lima, “LTL-Based Decentralized Supervisory Control of Multi-Robot Tasks Modelled as Petri Nets”, Proc. of IROS 2011 – IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 2011
[13] Bruno Lacerda, Pedro Lima, “Designing Petri Net Supervisors from LTL Specifications”, Proc. of the 2011 Robotics: Science and Systems Conference, Los Angeles, CA, USA, 2011
[14] José N. Pereira, Porfírio Silva, Pedro Lima, A. Martinoli, “Formalizing Institutions as Executable Petri Nets for Distributed Robotic Systems”, Proc. of ECAL 2011 – European Conference on Artificial Life, Paris, France, 2011