Formation State Estimation and Control
Multi-robot formation feasibility, formation control and formation state estimation have been subject of research at the ISLab since 2000.
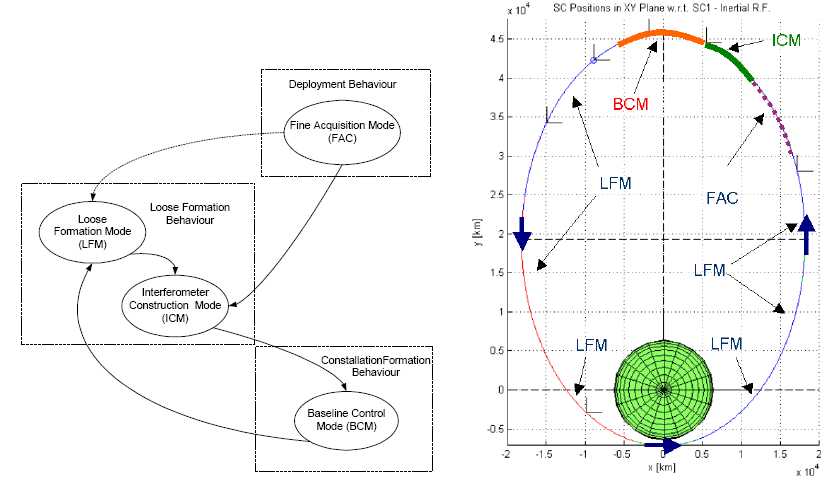
An integrated approach to Guidance, Navigation and Control (GNC) of formation flying spacecraft was developed under the project. The design process considers a 3-spacecraft mission in a reference Geostationary Transfer Orbit (GTO). A detailed definition of the mission framework, in terms of GNC modes and corresponding science and technology requirements, was provided by DEIMOS Engenharia. This, together with an analysis of the dynamic environment of the mission, establishes the inputs to the design of a low-thrust optimal relative configuration that minimises the fuel consumption and overall complexity.
The obtained solution is assessed in detail by means of an analysis considering perturbations acting over a spacecraft in Earth GTO. The GNC closed loop uses the results of the mission analysis and design process as specifications. An algebraic closed-loop algorithm is proposed for the Guidance and Control (GC) subsystem, minimizing the propellant consumption and ensuring collision avoidance. Using Pontryagin’s Maximum Principle, the GC algorithm provides the optimal trajectories from the current state until the target state, as well as the optimal control inputs to follow these trajectories.
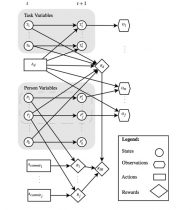
From the navigation standpoint, a formation flying s/c fleet endowed with relative distance sensors and RF communications can be considered to have two underlying networks: a communication network, where linked s/c communicate state estimates, and a measurement network, linking each s/c to all the s/c it measures the relative distances to. In general, a s/c measures distances and communicates them to any of its fleetmates. Nevertheless, it is desirable to reduce the number of measurements and especially the number of links in the communication network. The concept proposed in this work is to have each s/c measuring locally the distance to another fleet s/c (as expressed in the fleet measurements network), and transmitting its updated state estimates to another s/c (as expressed in the fleet communications network). The measurement network concerns the RF measurements of the distance with respect to another s/c. The communication network concerns the communication between pairs of s/c, in order to send/receive the full state estimate between two spacecraft of the fleet. The state estimates are considered as observations in the receiving s/c.
The Navigation algorithm is based, at each s/c, on an Extended Kalman Filter (EKF) for local measurements, and on a Covariance Intersection (CI) algorithm (plus the EKF prediction part) for the measurements communicated by its linked s/c in the communications network. The CI algorithm avoids the possible divergence of the EKF at the receiving s/c, due to correlation between measurements of the s/c in the fleet, by computing an upper bound for the covariance matrix of the fused variables. The price to pay is reduced estimation accuracy. Therefore, in the filtering step, the EKF is used when observations are measurements from the sensors, and the CI algorithm is applied whenever the observations are the state vector estimates from a s/c linked by the communications network.
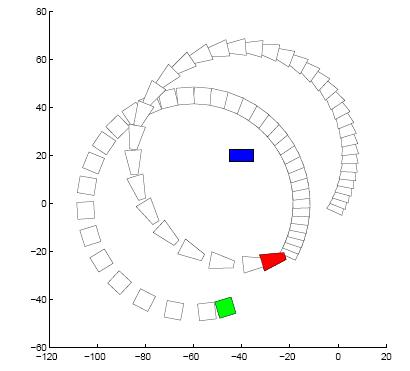
We extended Fiorelli’s and Leonard’s method of controlling a formation of holonomic vehicles to handle non-holonomic vehicle formations with a given geometry, compliant with nearby obstacles (including those represented by teammates). The vehicles are virtually linked to each other by the influence of artificial potentials that asymptotically stabilize the formation and keep all the robots separated by specified distances. A leader selected from the team, or a virtual reference point, is used to guide the team of autonomous vehicles throughout an area scattered with obstacles.
Each vehicle has access to the positions of all its teammates, and senses the obstacles within a limited range of its neighborhood. All robots will try to maintain the specified distance to the leader by using attractive potentials, while avoiding collisions among themselves and obstacles, by using repulsive potentials. To avoid falling in local minima of the potential fields, the vehicles will recall the n latest positions of the leader and use this information to move around the obstacle and keep the formation.
References
We developed a systematic framework for studying formation motion feasibility of multiagent systems. Algebraic conditions that guarantee formation feasibility (i.e., that the specified geometric constraints can be satisfied) given the individual robot kinematics were determined. Our framework also enables us to obtain lower dimensional control systems describing the group kinematics while maintaining all formation constraints.
References
- P. Tabuada, G. J. Pappas, P. U. Lima, “Motion Feasibility of Multi-Agent Formations”, IEEE Transactions on Robotics, Vol. 21 (3), pp. 387-392, 2005
- P. Tabuada, G. J. Pappas, P. U. Lima, “Feasible Formations of Multi-Agent Systems”, Proc. ACC2001 – American Control Conference, Arlington, VA, USA, 2001 – finalist of Best Student Paper Award
- Paulo Tabuada’s PhD thesis